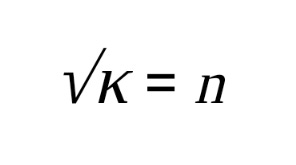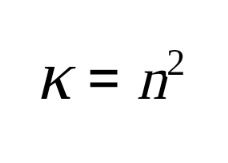The Dielectric Constant versus the Refractive Index
{and what effect their relationship has upon the formation of imaginary power}
The square root of the dielectric constant (κ) is equal to the refractive index (n) …
This could also be expressed as the dielectric constant is equal to the square of the refractive index …
Whenever a capacitor loses its capacitance, this results from the capacitor losing its ability to polarize an electric field within its dielectric materials sandwiched between its two conductive plates.
A capacitor can lose its capacitance by having its capacitance severely reduced to the point of it becoming nearly extinct. At this point, its capacitance literally turns off like a light switch and instead of entertaining the behavioral characteristics of capacitance, it entertains the behavioral characteristics of dispersion associated with a prismatic material measured by a refractive index.
So, all we have to do is select a capacitor whose value of capacitance is so low that it no longer functions as a capacitor capable of polarizing an electric field within its dielectric material.
Instead, what we find is that the dielectric material has become a prismatic material capable of dispersing the electromagnetic waves passing through it. This results in the splitting of an electromagnetic wave causing one half of the electromagnetic wave, which we know as current, to refract through the prismatic material, and the other half of the electromagnetic wave (associated with voltage) reflects off of the prismatic material because it cannot pass through the material. So, it inverts its polarity of voltage simultaneously with the passage of current through the prismatic material.
This simultaneity of the splitting of an electromagnetic wave causes it to become phase displaced by 180° between its current and its voltage. This is no longer Watts because it is no longer electric energy, it is no longer an electromagnetic wave. Instead of being watts, it is now VARs, namely: Volts-Amperes-Reactive.
Watts would have been capable of becoming subject to entropy. But VARs is not subject to entropy, because VARs is an imaginary expression of reactive impedance. So, VARs builds up its amplitude of imaginary power until there is sufficient amplitude of VARs to convert into heat upon its passage through simple resistance.
It could be inferred from this equation …
… that the dielectric constant (κ) possesses a property of two dimensionality by comparison to the refractive index (n) which is linear, namely: it merely possesses a singular dimensionality since the refractive index has to be squared in order for it to become equal to the dielectric constant.
This characteristic of the dielectric constant, to exhibit the properties of two dimensions, implies that it is capable of polarizing an electric field entering into a dielectric medium.
Meanwhile, the linearity of the refractive index suggests that it lacks the ability to polarize any sort of wave passing through it. So, instead of behaving like a dielectric material, a prismatic material merely disperses anything passing through it by way of refraction, and anything which cannot pass through it bounces off (reflects).
Since capacitors lead inductors in more ways than merely current leading voltage, whatever the capacitor is capable of or not capable of, the inductor must emulate in its own manner.
So, if capacitors lose the ability to polarize an electric field within their dielectric medium (and - thus - lose their ability to store an electric charge), then the consequence resulting from its association with an inductor causes the inductor to lose the ability to become saturated with current because the inductor is not being supplied with a constant source of current (displacement current) arising from the reactance of a capacitor.
Under these conditions, VARs has no choice but to bounce around within the system, never engaging the system, and (thus) never becoming engaged by entropy. And this makes sense, because VARs is not energy; it's merely the expression of reactive impedance which is totally imaginary.
For more information regarding how the refractive index is derived from the dielectric constant, please see the following web page …
The dielectric constant and the refractive index – (DoITPoMS, University of Cambridge)