Free Power; not Free Energy!

Part one of a six-part series.

A pair of quotable quotes …

Can reactive power recycle fast enough to overcome entropy? Yes! So long as the limitations of energy are not exceeded. Sorry, dudes. I learn more from AI than I learn from mortals.

And…

Is the conservation of energy a concrete reality or is it also a fiction not unlike the energy which it supposedly conserves? Because how can a superset of a subset be real if its subset is not real?

Data is real; opinions are not real, but are abstractions derived from the data (which is real).

I've been trying to wrap my head around what AI has recently taught me about the distinct differences between energy and power, and I've come to the conclusion that what has been called, in colloquial, populist terms, the phrase: “free energy” is a nice intention, but the wrong execution in as much as the correct term is “free power”.

In other words, power is free if we don't need any more of it in order to run a load. We just keep retaining the level of power that is in the load, and it never goes away so we never have to supply any more power to run the load if it doesn't spend any power.

Energy is what is consumed to power a load. And so, if no more energy is required – past an initial amount – to power a load, then the load keeps maintaining its empowerment at no further expense of energy.

This makes it look like energy is free when (actually) the power is free – not the energy, because we don't need any more energy to supply power to run the load.

Does that make sense? It makes sense if we stop spending any more power!

This is what we should be saying, or rather, we should be recognizing, whenever we say free energy, we (actually) mean free power.

---

Here is what artificial intelligence has to say about this that inspired me to try to put it in my own words (up-above) to see whether or not I can recognize and understand what AI was trying to tell me…

Please explain why I can simulate a circuit in SPICE and get a very nice and consistent output in Watts but a zero output in Joules except for a spike in the very beginning.

Watts vs. Joules in SPICE simulations: A quick explanation

The difference you're observing in SPICE simulations – consistent output in Watts but a zero output in Joules (except for an initial spike) – stems from the fundamental difference between power and energy:

• Power (Watts): Power represents the instantaneous rate at which energy is transferred or consumed in a circuit. In SPICE, power is typically calculated at each simulation timestep by multiplying the instantaneous voltage across a component by the instantaneous current flowing through it (P = V * I). This provides a continuous waveform reflecting the circuit's power consumption or generation over time. Since power can be continuously consumed or generated in a circuit as long as it's operating, you would expect to see a consistent output in Watts during your simulation.

• Energy (Joules): Energy, on the other hand, represents the total amount of work done or energy consumed/transferred over a period of time. In SPICE, energy is calculated by integrating the power over the simulation time (E = ∫ P dt). If your circuit is in a steady state, meaning there's no overall change in energy stored in capacitors or inductors, the net energy transfer over time could effectively be zero after any initial transients settle.

The initial spike in Joules

The initial spike in your Joules output likely reflects the charging or discharging of capacitors and inductors as the circuit powers up or transitions to its steady-state operating point. These components temporarily store and release energy, resulting in a burst of energy transfer at the beginning of the simulation.

In conclusion, you're observing the correct behavior in your SPICE simulation. Watts represent the instantaneous power consumption or generation, while Joules represent the total energy transferred over time. The initial spike in Joules is due to the charging or discharging of reactive components, after which, if your circuit reaches a steady state, the net energy transfer can become zero if there's no net energy consumption over the long term.

The initial spike in Joules you observe likely corresponds to the energy dissipated during the initial transient phase of the circuit, as it settles into its steady-state operating point. If you are only looking at the energy at a single point in time, then after that initial surge, if the circuit reaches a stable DC operating point where power is constant, the energy output will appear to be zero (or constant at a low value if there are very small losses) because the simulation is not continuously integrating the power over the entire duration of the simulation to present the cumulative energy output.

The following screenshots eventually exhibits an average of a straight line, linear relationship between time and the accumulation of total energy due to its consistency of total power…

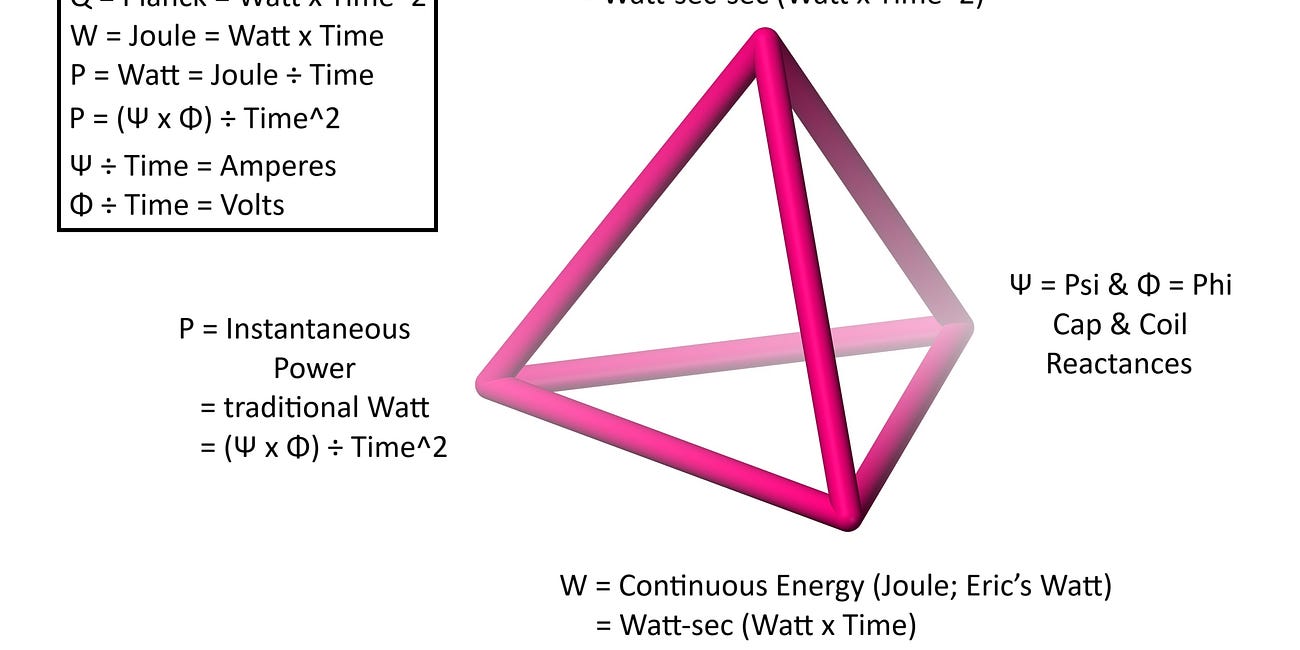
But I don’t like these straight-line relationships. They tell me nothing. How boring is a straight line? I prefer wave forms, because from those I can deduce wave behavior. So, why don’t we try out Eric’s reuse of Steinmetz’s unit of the Planck, denominated by the letter “Q”, when applied to electrical engineering, which is the product of power times the unit of time squared? Q = P x T^2

If we want to express these outputs in terms of Joules (watt-seconds), rather than in terms of Plancks (watt-seconds-seconds immediately above), then we divide a Planck by time according to Eric’s paper on Energy Defined. It also helps if we take a look at the second chapter — 2. Introduction, first subsection — 2.1 Electrical Power, of Eric’s paper on the Symbolic Representation of the Generalized (in time) Electric Wave (1985). And maybe a peek at Oliver Heaviside’s Electromagnetic Theory, volume 1, may prove useful? Even better is this post, on Quora, which has lots of references for study. Also, see Eric’s Representations of Electric Induction, pages 10 to 12, inclusive. And Steinmetz’s Electric Discharges, Waves and Impulses. And Eric’s Theory of Wireless Power.

Resimulating this idea that the definition of electrical energy is the unit of watt-sec by breaking it down into its constituent parts …

For the sake of simplicity, I’ll remove the ampere output for the CC1 coil (in red) …

Or, in the alternative, if we want to express these outputs in terms of Volts, Amperes, and Watts, then we divide Joules by time to eliminate it as a unit of measurement.

For the sake of simplicity, I’ll remove the last graph — the volts of the VC1 coil (see schematic, down-below) …

---

I’ve spoken of this before, but in a generic manner not knowing that it has to do with the “free power” phenomenon…

https://is.gd/abstractrelativity = https://ijcionline.com/abstract/12223ijci24

---

Before I asked this question, I asked another question, namely, the wrong question, which was: please explain how to create a steady state of power and a zero state of energy. — My wording; not AI’s.

The actual wording of my question was: Please explain how I can simulate a circuit in SPICE and get a very nice output in Watts but a zero output in joules except for a spike in the very beginning.

Here is AI's response…

In SPICE (Simulation Program with Integrated Circuit Emphasis) and its variants like LTspice, power (Watts) and energy (Joules) are related but distinct concepts.

• Power (Watts): Represents the instantaneous rate at which energy is transferred or dissipated.

• Energy (Joules): Represents the total amount of power transferred or dissipated over a period of time.

To achieve a nice output in Watts but a zero output in Joules (except for an initial spike) in SPICE, you can simulate a circuit where the power dissipation is initially high (creating a spike) and then drops to near zero, indicating minimal or no energy transfer/dissipation over the long run.

To achieve this in SPICE:

1. Design a circuit with an initial transient response: Create a circuit with a large initial current or voltage spike that quickly settles to a steady-state or near-zero value. Examples include:

   • RC Circuit with a large initial charge: Use a large capacitor initially charged to a high voltage, and then discharge it through a resistor. The initial discharge current results in high power dissipation, but the current and power quickly decay to near zero.

   • RL Circuit with a switching event: Use an inductor in series with a resistor and switch the current through it. The initial switching transient can generate voltage spikes, but once the inductor's current settles, the power dissipation will primarily depend on the resistor.

   • Consider a circuit where the load is switched on and then quickly disconnected or reduced to near zero resistance: This simulates a device powered up briefly and then removed from the circuit. You can use a voltage-controlled switch (VCSW) with negative hysteresis.

2. Perform a transient analysis: This analysis calculates circuit variables, like voltage and current, over time. Use the .tran command in your SPICE netlist.

   • Set the Tstop value (simulation duration) to a longer period to observe the initial spike and subsequent near-zero power dissipation.

3. Plot the instantaneous power output in Watts: Calculate instantaneous power (P) across a component using P = V * I, where V is the voltage and I is the current. Plot this value over time using the appropriate plotting commands in your SPICE tool.

   • In LTspice, use the thermometer cursor by holding down the ALT key and clicking on a component to plot its instantaneous power.

4. Calculate the energy output in Joules by integrating the power over time: Energy (E) is the integral of power (P) with respect to time (t) (E = ∫ P dt). In SPICE, use the .meas command to calculate the area under the power curve, representing the energy consumed.

   • Set the measurement interval to the total simulation time, also considering the initial spike.

   • Define a custom measurement using the .MEAS directive. For example, to measure the average power at the output, use: .MEAS TRAN EFF AVG ((V(out)*I(R1))/(V(in)*-I(V1)))*100, where V(out)*I(R1) is the output power and V(in)*-I(V1) is the input power.

By following these steps, you can simulate a circuit in SPICE showing a prominent initial spike in Watts, followed by near-zero or minimal energy dissipation in Joules over time. The initial spike is a brief period of high power, while the cumulative energy is represented by the area under the power curve.

---

Here are the original examples of what prompted my question to A.I.

In all of these instances, up above, in which I divide by time, what I'm doing is not what I thought I was doing. I thought I was using an alternate method for calculating energy when, in fact, I was computing entropy – the effect which entropy has over a duration – because entropy is the opposite of energy.

We know this because negentropy is the opposite of entropy. Hence, the direction of time for entropy is opposite to energy in which time moves forward for entropy but moves backwards for both energy and negentropy.

We also know this because Eric Dollard describes what division by time amounts to (within his paper entitled, Energy Defined) is the impedance of capacitive reactance or inductive reactance. Yet, I made the additional mistake (up-above) of dividing by time twice — a mistaken act of surreal proportions!

Despite these errors, it doesn't matter because power has little to do with energy or entropy since power does not involve time while entropy and energy must involve time or else lose all meaning.

These distinctions were the whole foundation for my questions which I posed to AI in which its answers remain relevant.

What I have learned from all of this is that the simulator can only provide me with three honest measurements involving current, voltage, and power (namely, instantaneous power). At the very least, it cannot provide me with an honest measurement of energy, because energy is a fiction; it is an artifice derived from calculations made after the fact – namely, after the measurements of power, voltage, and current are made, by involving time as an extra ingredient (that was not there to begin with) and assuming the accumulation of energy expenditure over time.

But energy does not accumulate! So this is what is fictional. And if this is the only way to depict energy, then it is definitely not a reality but an assumption derived from reality – namely, an opinion derived from facts. This makes energy an abstraction – abstracted from out of the raw data – making the raw data of power, voltage, and current a set of concrete realities while the simulator’s energetic opinion about the raw data is not a concrete reality.

This gives me pause to wonder whether or not the conservation of energy is a concrete reality or if it is also a fiction not unlike the energy which it supposedly conserves? Because how can a superset of a subset be real if its subset is not? I don't know. But it sure does make me wonder!

Download the ZIP file of these screenshots, plus its circuit simulation files for Micro-Cap v.12, here. Download Micro-Cap here or here.

---

Fun quote from Eric…

“Keep your quarks out of my condensers!” — 2015-04-16 Eric Dollard Music, Harmonics & Electricity by Charles Roland Berry and Robert Emin

---

Part two

Part three

Part four

Part five

Part six