Conservation of Energy cannot relate to Idealized Components
It should be renamed, Accounting for the Loss of Energy in an Imperfect World.
Reactive components are not “fence sitters”. They are not capable of maintaining the consequences of their reactions especially if they are ideal (incapable of losing energy).
Just because we define an “ideal transformer” as being incapable of losing energy does not make it so, because an ideal transformer is a generator while a non-ideal transformer absorbs energy and dissipates it as a loss.
Thus, an ideal transformer is anything but a passive component. The same could be said of an ideal capacitor. Their combination generates electricity without the need for a prime mover injecting energy from outside the system to any great degree, namely: their production of electricity is greater than whatever it takes to initiate this production.
There is never a time when inductance, alone, exists. Neither is there ever a time when merely capacitance exists. Both coexist at all times along with frequency, various resistances, and a duration over which all of this transpires.
For instance, a length of wire possesses inductance due to its length. It possesses capacitance due to the thickness of its insulation versus the total surface area of that length of wire. And it possesses resistance based on its girth versus its length (resulting in a wire gauge which we assign it to) plus the inherent resistance of its material composition.
We may not see any appreciable gain of energy due to entropy overwhelming the overall situation, but that doesn’t mean that ideal reactive components don’t generate energy all of the time.
It’s like a pool of water sitting peacefully on the sidewalk, or on top of some other surface, slowly evaporating…
Just because it looks so peaceful (we don’t see any violent boiling going on when we’re looking at it with our naked eye), doesn’t mean it isn’t boiling…
It’s boiling, alright. We just can’t see it since there are so few molecules of water undergoing a change-of-state (from a liquid into a gaseous condition) that we misdiagnose the situation as being “not boiling”, but “evaporating”.
Yet, the two processes of boiling water versus its evaporation are no different from each other except with regard to how long it takes to deplete all of the liquid water.
It’s a question of statistics, not physics, since we can’t see how many molecules of water are cavitating (converting into gaseous vapor) versus how many molecules of water are not cavitating.
Likewise, is it true with all reactive components. By their inherent nature, they cannot support the Conservation of Energy in which “energy IN equals energy OUT” under ideal conditions in which no voltage is lost (due to capacitor leakage), nor does any magnetism dissipate (due to coil leakage), because the combination of capacitive reactance and inductive reactance always produces some energy no matter how small and insignificant it may appear to be in contrast to how much entropy wipes out this puny gain.
I’ve been vexing1 for quite some time, now, over Paul Falstad’s ideal transformers2 modeled within the context of his online simulator.3
It was a waste of time to vex over it since his transformers are capable of the generation of power whenever they’re coupled to appropriate capacitances since both his capacitors4 and his transformers are “ideal” in that they are not capable of losing any energy due to leakages, etc.
Even if I were to replace his transformer with a short between two air-core coils,…
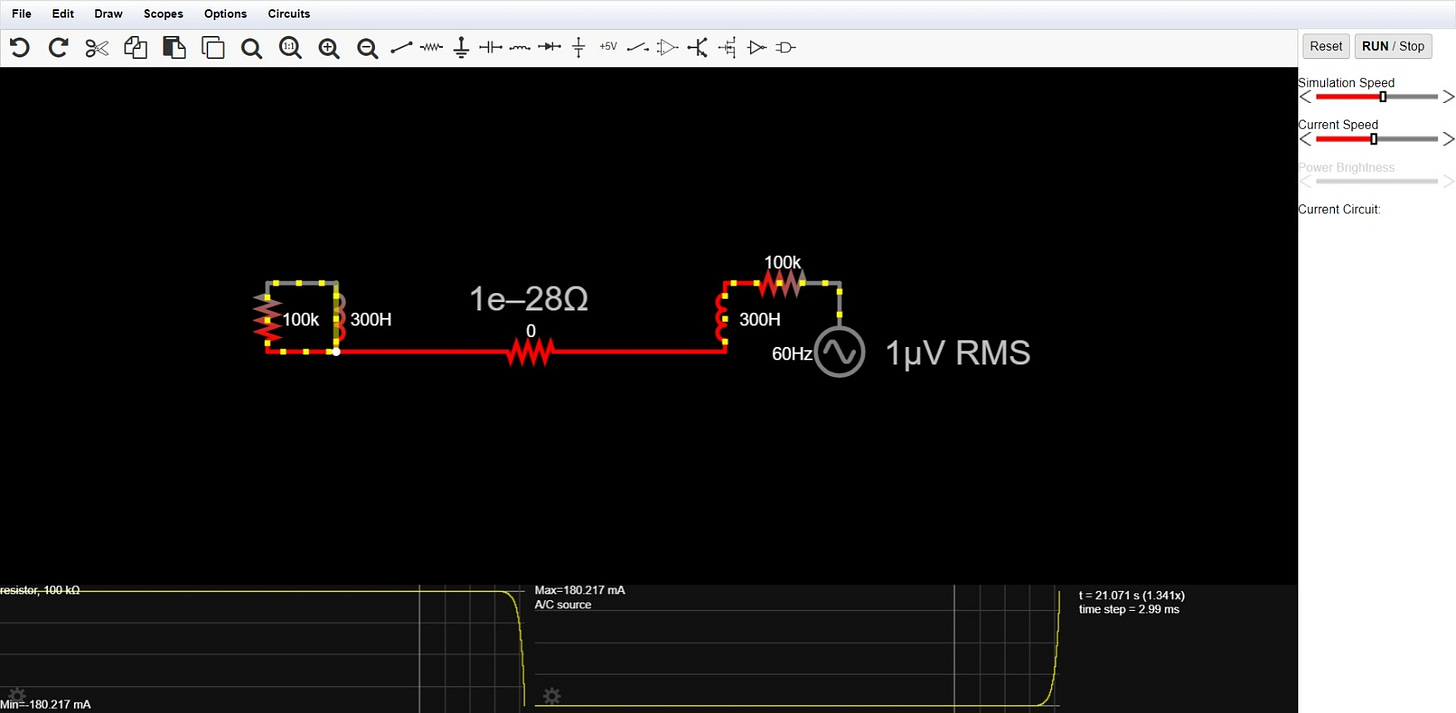
Figure 1 – first version.5
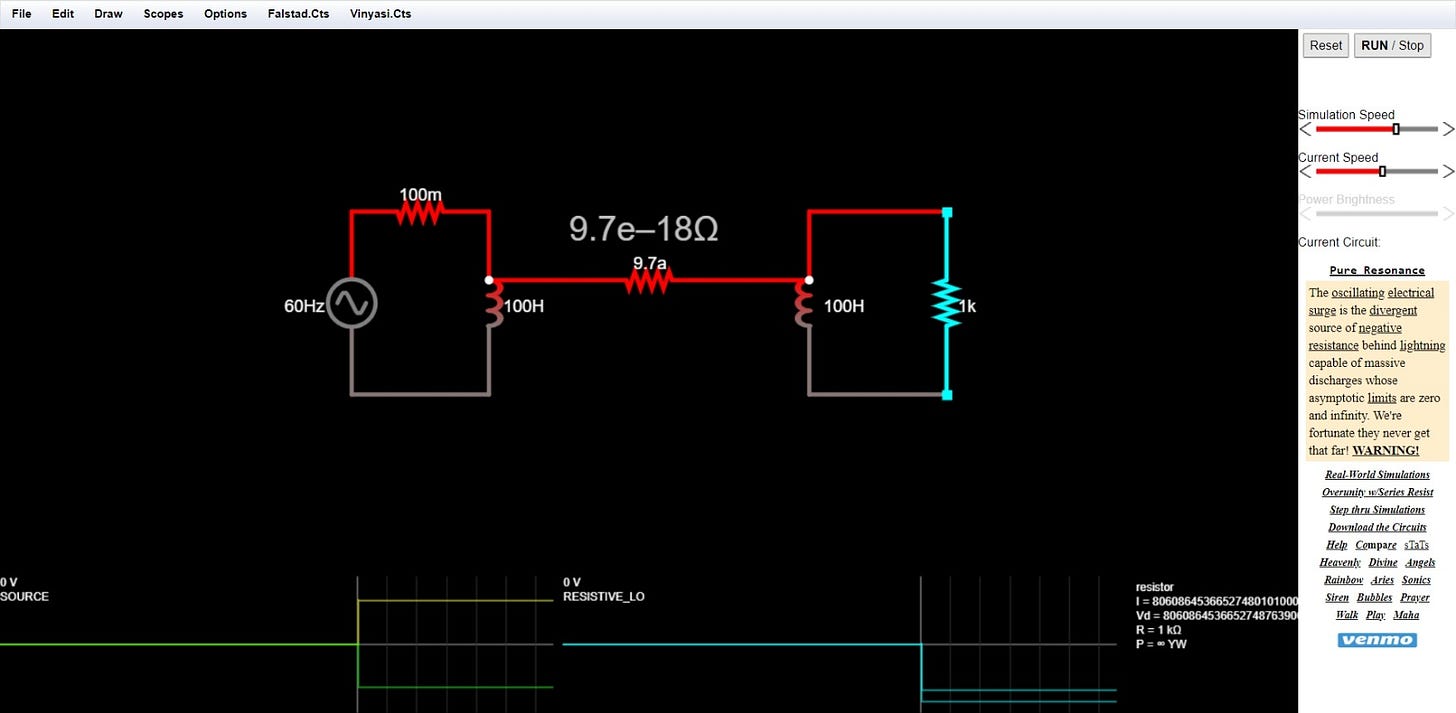
Figure 2 – second version.6
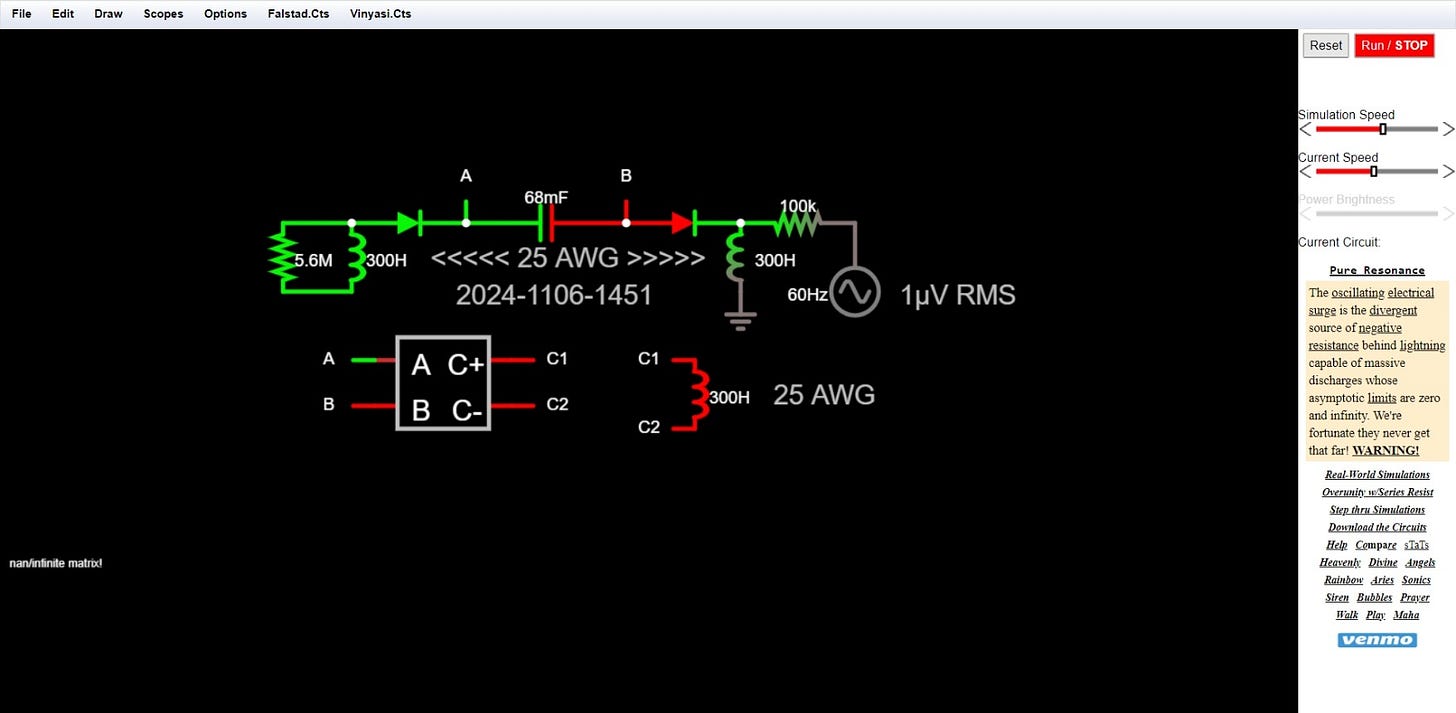
Or else, if I replace his transformer with some diodes, capacitors, air-core coils, and a voltage-controlled current source, …
Figure 3 – instantaneous kaboom (after simulating a single time-step of seven microseconds).7
Despite all of these replacements, I will still get overunity8 due to the ideal condition of his entire simulator.
It’s unavoidable due to his simulator’s idealistic condition.
It’s unavoidable due to the inherent nature of reactive components if they subscribe to an ideal condition.
This is why the Conservation of Energy is not valid under “ideal” conditions.
Wait a minute…
I thought that the Conservation of Energy was an ideal condition, in and of itself, by being universal in its application (without exceptions).
What’s going on?
Controversial reference #1…
The Relativity of Energy and the Reversal of Time is a Shift in Perspective9
Ambiguous reference #2…
An isolated system10 obeys the conservation law11 that its total energy–mass stays constant. Most often, in thermodynamics, mass and energy are treated as separately conserved.
Because of the requirement of enclosure, and the near ubiquity of gravity, strictly and ideally isolated systems do not actually occur in experiments or in nature. Though very useful, they are strictly hypothetical.12 13 14
Classical thermodynamics is usually presented as postulating the existence of isolated systems. It is also usually presented as the fruit of experience. Obviously, no experience has been reported of an ideally isolated system.
This is a contradiction of first principles in as much as the Conservation of Energy is usually presented as being an “a priori” (first principle) among many other principles adorning modern-day physics.
Yet, only under non-ideal (less than accurate) conditions will reactive components obey this ideal condition of energy-conservation.
And Wikipedia admits to the predicate of energy-conservation (within the context of isolated systems) as being anything other than existential. Isolated systems are hypothetical.
This makes the Conservation of Energy a contradiction in that it is not ideal and at the same time be capable of supporting reactive components (in their ideal state) despite its status as a hypothetical “Law”.
This makes reactive components (capacitors and coils of wire which we can purchase or build from available materials) open to the possibility of being capable of supporting the Conservation of Energy provided that these reactive components are not reactive (despite their being advertised as such by their manufacturers). Another contradiction…
What makes this even more difficult to appreciate is the fact that the imaginary power spawned by electrical reactance is no different than the imaginary reactance which spawns it.
Consider the mathematical relationships well known to electrical engineers and available to us lay people on Wikipedia...15
Both reactance X and resistance R are components of impedance Z.
where:
R is the resistance, measured in ohms. It is the real part of the impedance: R=Re(Z)
X is the reactance, measured in ohms. It is the imaginary part of the impedance: X=Im(Z)
j is the square root of minus one, usually represented by i in non-electrical formulas. j is used so as not to confuse the imaginary unit with current, commonly represented by i.
Consequently, how much difference is there between complex impedance (Z) and imaginary reactance (X), and the imaginary power which results therefrom, whenever imaginary power dominates the real and imaginary portions of complex power? Not a whole lot!
Thus, the more imaginary power becomes available over the duration of a parasitic oscillation, the more reactance (namely, the more reactive impedance), there is available for spawning more imaginary power at a faster pace of its creation due to the accumulation of imaginary reactance (X). This is why the addition of resistances, in and among reactive components, can augment this process by adding to the total impedance generated by the reactive components.
Energy cannot be created nor destroyed, but that says nothing about the creation or destruction of imaginary power which is not energy even though it can be converted into energy (by passing it through a resistor acting as a resistive heating element - as merely one example) to boil water and rotate a steam turbine which is shackled to the axle of a rotary electric generator.
A second example (of the conversion of imaginary power into real power) would be to pair two windings, electrically connected to each other in parallel with each other, and each winding is wound in a direction which is opposite the other winding, also known as: cross-winding (or counter-opposed winding) in which one winding is clockwise and the other is counterclockwise. The reactive amperage of one winding creates a field (a magnetic field) of reactive amperage which mingles with the magnetic field of reactive voltage of the opposed winding. The same is true for all of the other reactive relationships between the two windings.
Thus, a blend of imaginary reactive components of electricity unite to form a total field of real power (measured as negative Watts) even though the individual components which spawned these fields are imaginary.